几何学中,折叠作为一种直观的动态操作,不仅为探索图形性质提供了实验性视角,更成为连接抽象定理与具象认知的桥梁。以等腰三角形为载体的折叠问题,既揭示了轴对称变换的普遍规律,又衍生出勾股定理、三线合一等核心知识点的综合应用。本文将从教学设计的底层逻辑出发,结合折叠问题的解题策略,探讨如何通过几何变换深化学生对三角形性质的理解。
一、等腰三角形性质与折叠基础
等腰三角形的本质特征决定了其在折叠问题中的特殊地位。根据沪科版教材的教学设计,学生通过将两腰叠合可直观发现“等边对等角”的基本规律。这一过程中,顶角平分线、底边中线和高线三线合一的特性,使得折叠后形成的对称轴天然具备多重几何属性。
在具体教学实践中,可设置将等腰三角形纸片沿顶角平分线折叠的操作。当学生观察到折痕同时成为底边的垂直平分线时,轴对称图形的本质特征——对应点连线被对称轴垂直平分——便自然呈现。这种通过折叠验证定理的方式,比传统演绎证明更符合初中生的认知发展规律。
以沪科版教材中的典型例题为例:已知△ABC中AB=AC=BC,通过折叠构造等边三角形的过程,不仅验证了推论2“等边三角形各角均为60°”,更通过纸片展开后的折痕分析,建立起边角关系的可视化认知模型。这种将定理证明转化为折叠实验的教学策略,有效降低了抽象几何概念的认知门槛。
二、折叠问题的几何原理剖析
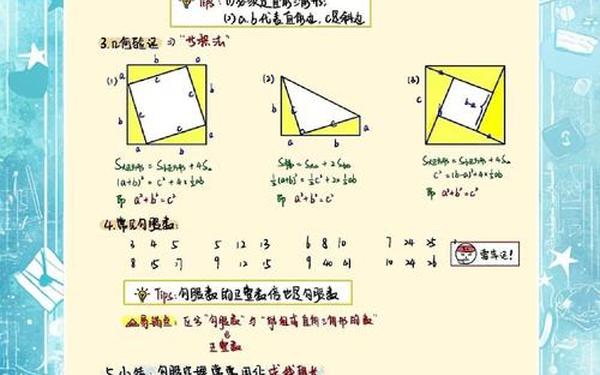
折叠的数学本质是全等变换,这一过程遵循严格的几何定律。三余弦定理(又称折叠角公式)指出:当平面外一点B的投影为A时,∠COB=arccos(cos∠AOB·cos∠AOC)。这一定量关系为求解复杂折叠问题提供了普适性工具,如在正方形纸片沿对角线折叠的案例中,该定理可快速计算出折后角度为120°。
在动态折叠问题中,勾股定理常与全等变换形成解题闭环。以直角三角形DEC折叠至DEF为例,通过设CE=x建立方程(8-x)²=3²+x²,完美演绎了代数与几何的融合。此类问题训练中,教师需引导学生识别折叠前后的不变关系:对应边相等(BE=B'E)、对应角相等(∠B=∠B')以及对称轴垂直平分对应点连线(CC'⊥MN)等关键特征。
值得关注的是折叠引发的特殊点问题。当点A'在BC边上移动时,其轨迹受双重约束:既要满足轴对称条件,又需符合目标三角形的存在性要求。这类问题往往需要构建直角三角形模型,通过三角函数关系式tanθ=对边/邻边建立动态方程,培养学生在变化中把握不变量的高阶思维。
三、教学策略与思维培养路径
优质教学设计应实现从具象操作到抽象思维的阶梯式跨越。在浙教版《几何图形》起始课案例中,通过长方体纸盒的拆解折叠,学生直观体会了点、线、面、体的转化关系。这种基于实物操作的概念建构方式,为后续学习三角形折叠奠定了空间想象基础。
问题链设计是提升探究深度的关键。某优秀教案设置如下递进式问题组:“折痕具有哪些几何性质?”“如何证明折叠后的三角形全等?”“当折痕位置变化时,极值点如何确定?”这些问题引导学生从验证性实验转向发现性研究,契合《义务教育数学课程标准》强调的“四基”培养要求。
分类讨论能力的培养需依托典型例题。例如在矩形ABCD折叠问题中,区分点A'落在BC边或其延长线的两种情形,要求学生同时考虑几何约束与代数条件。此类训练强化了思维严密性,使学生理解数学结论的成立往往需要附加条件限定。
四、前沿探索与教学启示
当前教学研究正朝着跨学科整合方向推进。“直角三角形背景下的折叠问题”专题课例展示了一种创新模式:通过折纸操作引出数学问题,继而用几何画板动态演示变量关系,最后回归数学建模解决实际问题。这种“做中学”的理念,将STEAM教育思想自然融入几何教学。

未来研究可深入探讨折叠问题与计算思维的关联。例如将折痕方程编程可视化,或开发增强现实(AR)辅助教学系统。已有实践表明,利用GeoGebra软件模拟折叠过程,能有效突破传统教学中的空间想象瓶颈,使三余弦定理等抽象原理获得多维度呈现。
教师专业发展方面,建议构建区域性教学资源库,收录典型折叠问题案例。某教研团队开发的“一图一课”资源体系,以基础图形衍生变式问题,既保持了知识的结构化,又实现了思维的进阶性发展,这种经验值得推广。
从等腰三角形的性质教学到复杂折叠问题的求解,几何教育始终在直观感知与逻辑推演之间寻求平衡。当代教学设计更需注重技术融合,将折叠操作蕴含的数学原理,转化为发展学生空间观念、推理能力和创新意识的思维载体。未来的研究应继续深化折叠问题与其他数学分支的联结,探索其在拓扑学、离散数学等领域的教育价值,为核心素养导向的数学课程改革提供新范式。

