在小学高年级数学学习的关键阶段,五年级教材通过螺旋式上升的知识结构构建起数学思维的基础框架。当我们将目光聚焦于人教版五年级数学教材,会发现上册第三单元《小数除法》与下册第三单元《长方体和正方体》共同构成了数理思维与空间观念的双重培养体系。借助思维导图这一可视化工具,学生不仅能将零散的知识点串联成网,更能通过图形化表达深化对数学本质的理解,这种认知重构方式正在成为突破数学学习瓶颈的利器。
知识体系的模块化梳理
五年级上册第三单元《小数除法》围绕"商不变性质"这一核心原理展开,通过思维导图可将知识模块分解为计算法则、循环小数、近似值处理三大分支。以"除数是小数的除法"为例,思维导图能清晰展示计算步骤:先将除数转化为整数,再按整数除法法则计算,最后处理小数点位置。这种模块化呈现方式,使学生直观理解"转化思想"在数学运算中的普遍应用。
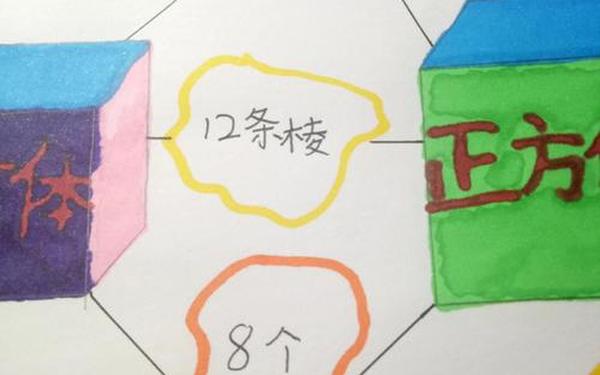
下册第三单元《长方体和正方体》的知识图谱构建则遵循"特征—公式—应用"的逻辑链条。思维导图将12条棱的特征与表面积计算公式(S=2(ab+ah+bh))、体积公式(V=abh)建立联系,同时标注特殊形态如无盖长方体的表面积计算方法。通过颜色区分概念与公式,学生能快速定位知识层级,避免混淆棱长总和与表面积计算。
逻辑关系的可视化呈现
在因数与倍数知识板块中,思维导图以放射状结构展示2、3、5倍数特征的判别方法。例如将"个位偶数"与2的倍数相连,"各位和是3的倍数"与3的倍数建立关联,这种视觉编码强化了数字特征的记忆锚点。对于质数与合数的辨析,思维导图通过列举20以内质数(2、3、5、7等),配合"因数个数"的对比,使抽象概念具象化。
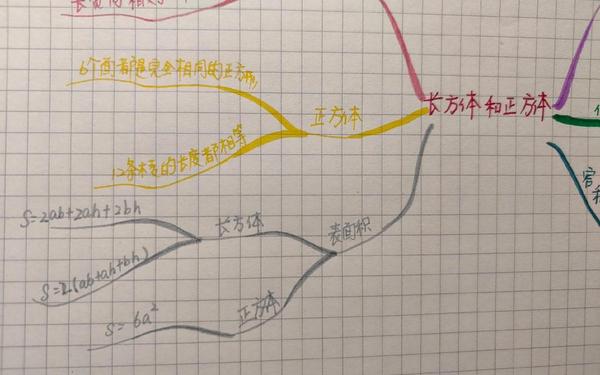
空间几何单元中,思维导图通过三维展开图与二维平面图的对照演示,帮助学生建立立体与平面的转换思维。在展示长方体特征时,采用双气泡图对比长方体与正方体的异同:前者相对面相同,后者所有面全等;长方体棱长总和公式((a+b+h)×4)与正方体(12a)形成公式对比,这种并置结构强化了特殊与一般的数学关系认知。
重难点突破的有效工具
针对小数除法中的循环小数理解难点,思维导图可设置"发现循环节—标注省略号—近似值取舍"的思维路径。例如将28÷18=1.555...表示为1.5(•),配合颜色标注循环节,再延伸出"四舍五入"的保留位数规则,这种多维度呈现化解了抽象符号的理解障碍。在解决实际问题时,导图分支可添加购物找零、油量计算等生活案例,强化数学应用意识。
在立体几何的棱长计算教学中,思维导图通过逆向思维训练提升解题能力。例如已知棱长总和求高(h=L÷4-a-b),导图用箭头标注公式变形过程,配合铁丝制作长方体框架的实践案例,将公式记忆转化为问题解决工具。对于表面积计算的易错点,特别标注"无盖"情况的公式调整(S=ab+2(ah+bh)),通过醒目的警示图标提醒学生注意语境条件。
跨单元知识的有机串联
思维导图的超链接功能可实现知识迁移,例如将小数除法中的估算策略与下册分数加减法的通分技巧建立联系。在解决"油箱容积"问题时,既需要上册的体积计算能力(V=abh),又涉及下册的容积单位换算(1L=1dm³),导图通过跨单元连接促进知识融合。这种整合式学习有助于学生理解数学知识的网状结构,而非孤立的知识点堆积。
在因数倍数与分数知识的衔接处,思维导图展现强大的整合能力。通过将最大公因数(GCD)与约分操作关联,最小公倍数(LCM)与通分方法串联,形成从整数特性到分数运算的完整认知链条。这种跨年级的知识映射,为后续学习异分母分数加减法奠定坚实基础,体现思维导图在构建知识体系中的独特价值。
通过系统化的思维导图构建,五年级学生不仅能掌握具体的数学知识,更重要的是培养结构化思维能力和知识迁移能力。教师在教学实践中可借鉴网页37中的案例,利用树图等工具设计分层递进的导图模板。未来研究可进一步探索动态思维导图与虚拟现实技术的结合,在三维空间中直观演示几何体的展开与折叠,这将是数学可视化教学的新方向。对于教育工作者而言,掌握思维导图的设计原理与实施策略,将成为提升数学教学效能的关键突破口。

