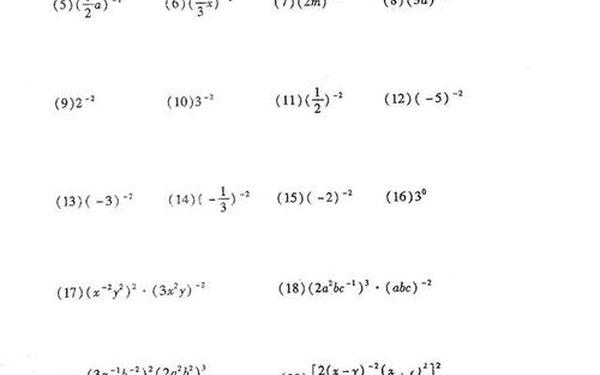一、核心知识点
1. 勾股定理与实数
勾股定理:直角三角形两直角边的平方和等于斜边平方,即 ( a^2 + b^2 = c^2 ),逆定理可判断三角形是否为直角三角形。常见勾股数组如 (3,4,5)、(5,12,13) 等。
实数:包括有理数和无理数,掌握实数的运算(加减乘除、乘方开方)及性质(绝对值、相反数等)。
2. 代数与方程
分式方程:解法步骤为去分母、解整式方程、检验增根。例如方程 ( frac{1}{x-2} = frac{6}{2x-12} ) 需转化为整式方程后求解。
因式分解:常用方法包括提公因式法、公式法(平方差、完全平方公式)及分组分解法。例如 ( x^3
2x^2y + xy^2 = x(x-y)^2 ) 。
3. 几何图形
三角形:内角和为180°,外角性质(外角等于不相邻两内角和),全等三角形的判定(SSS、SAS、ASA等)。
四边形与多边形:平行四边形、矩形、菱形等特殊四边形的性质与判定,多边形内角和公式 ( (n-2)
imes 180° ) 。
4. 函数与图像
一次函数:表达式为 ( y = kx + b ),图像为直线,重点掌握斜率与截距的意义及其应用。
平面直角坐标系:点的坐标表示、轴对称点的坐标变换规律(如关于x轴对称时横坐标不变,纵坐标取相反数)。
5. 数据与概率
数据统计:计算平均数、中位数、众数,理解方差和标准差的意义(方差越小数据越稳定)。
概率初步:简单事件的概率计算,例如掷骰子时某点数的概率为 ( frac{1}{6} ) 。
二、典型计算题
1. 代数运算
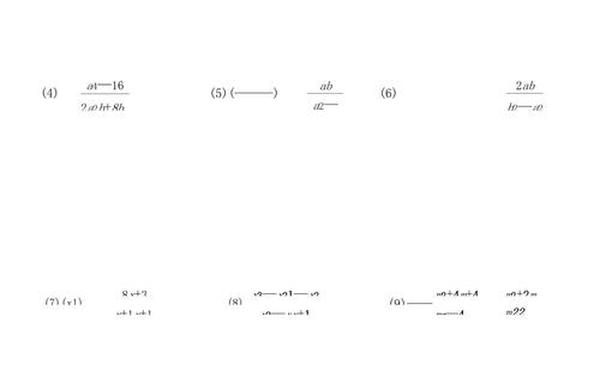
分式化简:
[
left( frac{x+2}{x^2-4}
frac{1}{x-2} right) div frac{2}{x-2} = frac{1}{x+2}
]
需注意通分和约分步骤。
整式乘除:
[
3x^2y cdot 6xy^3 div (-3x^2y^2) = -6y^2
]
需按顺序进行幂运算和系数处理。
2. 方程求解
分式方程:
[
frac{1}{x-2} + 1 = frac{3}{2-x}
]
解:去分母得 ( 1 + (x-2) = -3 ),解得 ( x = -2 ),需检验是否为增根。
一元二次方程:
[
x^2
5x + 6 = 0 Rightarrow (x-2)(x-3) = 0
]
解得 ( x = 2 ) 或 ( x = 3 ) 。
3. 几何计算
勾股定理应用:已知直角三角形两直角边为3和4,求斜边长为5。
三角形面积:底边6cm,对应高4cm,面积 ( frac{1}{2}
imes 6
imes 4 = 12 ,
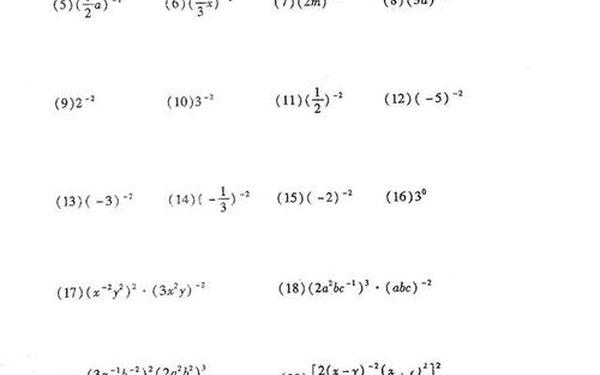
ext{cm}^2 ) 。
4. 函数解析
一次函数图像:若 ( y = 2x + 1 ),当 ( x = 0 ) 时 ( y = 1 ),图像经过点 (0,1),斜率为2。
三、学习建议
1. 知识点整合:结合思维导图梳理勾股定理、函数等模块的关联性。
2. 计算强化:每日练习分式运算、因式分解等易错题型,推荐使用北师大版课后习题巩固。
3. 错题分析:整理方程求解中的增根问题及几何证明的逻辑漏洞,针对性突破。
如需完整习题集或电子课本,可参考人教版、北师大版教材配套资源或专业教辅网站(如学科网、知乎专栏)。