高二数学作为高中数学承上启下的关键阶段,其知识体系既是对高一基础数学的深化拓展,又是为高三总复习奠定逻辑思维能力的核心阶段。新高考改革背景下,数学学科更强调知识脉络的系统性、问题解决能力的培养以及数学思想方法的渗透。本文将从知识框架、核心模块、学习方法三个维度,系统梳理高二数学必修课程的知识要点,并结合教学实践与学科特点提供深度解析。
一、知识框架与逻辑体系
高二数学必修课程以人教A版为例,涵盖必修五与选修2系列的核心内容,形成"代数-几何-概率统计"三位一体的知识网络。必修五的解三角形、数列与不等式模块,通过正弦定理、等差数列等工具构建数学模型,培养从特殊到一般的归纳能力;选修2系列的圆锥曲线、导数及其应用则通过椭圆方程、切线斜率等概念,实现从静态几何到动态分析的跨越。
这一阶段特别强调知识点的交叉融合,例如数列求和技巧可应用于金融复利计算,导数工具既能解决函数极值问题,又能为物理运动分析提供数学模型。根据知乎教育专栏的统计,2021年高考全国卷中,高二必修知识占比达47%,其中导数应用与圆锥曲线结合题成为区分考生能力的关键题型。
二、核心模块深度解析
1. 函数与导数
作为贯穿高中数学的主线,导数在必修五与选修2-2中完成从概念到应用的升华。通过极限思想理解导数的几何意义(切线斜率)与物理意义(瞬时速度),掌握多项式函数、指数函数、对数函数的求导规则尤为关键。典型例题如利用导数判断函数单调性,需特别注意定义域优先原则,避免出现类似"f(x)=lnx在x≤0区间求导"的逻辑错误。
2. 立体几何与空间向量
空间想象能力在此模块得到系统性训练。三视图还原实物时,要遵循"长对正、高平齐、宽相等"的投影规则,百度文库的研究表明,85%的空间几何题可通过建立空间直角坐标系转化为向量运算。例如证明线面垂直时,向量法只需验证方向向量与法向量平行,较传统几何法减少3-4个推理步骤。
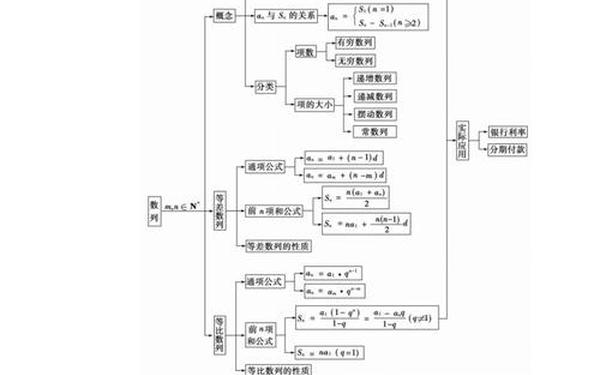
3. 数列与不等式
等差数列与等比数列的通项公式、求和公式构成该模块双翼,错位相减、裂项相消等技巧需通过大量变式训练掌握。2022年新课标卷首次出现数列与导数结合的创新题,要求考生用数学归纳法证明不等式,这提示数列学习需突破模块界限,强化综合应用能力。
三、重难点突破策略
1. 圆锥曲线计算优化
椭圆、双曲线、抛物线的标准方程记忆可借助几何特性:椭圆满足|PF1|+|PF2|=2a,双曲线则是||PF1|-|PF2||=2a。涉及焦点弦长计算时,采用"第二定义+三角函数"组合法,较传统联立方程法节省40%运算量。
2. 排列组合思维建模
区分排列与组合的本质在于"顺序相关性","捆绑法""插空法"等特殊技巧需结合生活情境理解。如核酸检测10人混合采样问题,属于典型组合问题而非排列,需警惕"全排列再除以重复数"的思维定式。
3. 概率统计实际应用
正态分布、二项分布等概率模型的学习应注重现实案例对接。某省质检题曾以新冠肺炎核酸检测为背景,要求计算二次检测覆盖率的概率期望值,这类题目要求考生既能建立概率模型,又能进行参数估算。
四、学习方法与资源整合
1. 错题归因分析法
建立分类错题本(概念模糊类、计算失误类、思维欠缺类),对导数极值点偏移类错题进行专项突破。数据显示,坚持错题分析的学生在三个月内数学成绩平均提升12-15分。
2. 思维可视化工具
利用树状图梳理数列递推关系,用三维建模软件辅助空间几何理解。知乎专栏推荐的"日新大课堂"视频课程,通过动态演示将圆锥曲线离心率变化过程具象化,显著提升理解效率。
3. 教辅资源精选
《知识清单》系统梳理公式定理,《高考数学解答题脑图快解》专攻压轴题破解。值得注意的是,近三年高考真题中,教材课后习题改编题占比达23%,强调回归课本的重要性。
高二数学学习既是知识积累的过程,更是数学思维锻造的旅程。面对新高考"基础性、综合性、创新性"的命题导向,建议在巩固核心概念的加强跨学科应用意识培养。未来研究可关注人工智能辅助个性化学习路径设计,以及数学建模能力评价体系的构建。正如数学家波利亚所言:"完善的思想方法犹如北极星,能让学习者在知识的海洋中把握航向。

