1. 教学目标与指导思想
目标:系统掌握初中数学核心知识,提升逻辑推理、运算能力及解决实际问题的能力,为中考打下坚实基础。
重点方向:
夯实代数基础(如一元二次方程、二次函数、不等式等);
强化几何推理(相似三角形、圆的性质、四边形等);
培养应用能力(概率统计、函数建模、数形结合等)。
2. 教学内容与进度安排
核心章节:
代数:一元二次方程、二次函数、反比例函数;
几何:圆的性质与计算、相似三角形判定、四边形综合题;
统计与概率:数据分析、概率计算。
三轮复习法:
第一轮(基础复习,2-4月):梳理教材知识点,侧重公式定理记忆与基础题型训练(如解方程、几何证明)。
第二轮(专题突破,5月):针对高频考点(如二次函数应用题、圆的综合题、动态几何)进行专题训练,强化解题技巧。
第三轮(模拟冲刺,6月):通过中考真题及模拟卷训练,查漏补缺,优化答题策略和时间分配。
3. 教学方法与策略
分层教学:根据学生水平(A/B/C层)设计差异化练习,如基础题巩固、中档题拓展、难题突破。
错题管理:建立错题本,分类整理典型错误(如计算失误、审题偏差),针对性强化训练。
课堂互动:采用“讲练结合”模式,每节课预留15分钟限时训练,提升课堂效率。
二、初三中考数学重点知识归纳
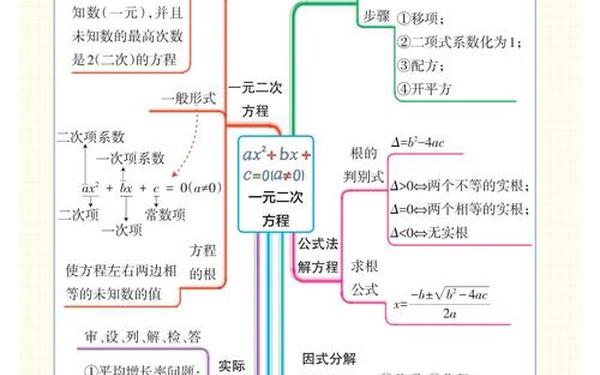
1. 代数模块
一元二次方程:解法(配方法、公式法、因式分解法)、根与系数关系(韦达定理)、实际应用题(如增长率问题)。
二次函数:图像性质(顶点、对称轴)、最值问题、与方程/几何结合的综合题(如抛物线交点问题)。
不等式:一元一次不等式组解法、数轴表示解集、实际情境应用(如方案优化)。
2. 几何模块
圆:垂径定理、切线性质、圆周角定理、弧长与扇形面积计算;
综合题型:圆与三角形/四边形结合的动态几何问题。
相似与全等:相似判定(AA/SAS/SSS)、位似变换、相似比与面积比关系。
解直角三角形:锐角三角函数(sin/cos/tan)、仰角/俯角实际应用题。
3. 函数与统计
反比例函数:图像性质(双曲线)、与几何图形结合的面积问题。
概率与统计:平均数/方差计算、概率公式(古典概型、树状图法)、数据分析与图表解读。
4. 高频易错点
计算规范:分式化简、根式运算中的符号处理;
几何陷阱:辅助线添加不当、相似三角形对应边混淆;
综合题策略:函数与几何交叉题的步骤拆分(如先求解析式再分析几何关系)。
三、复习建议与资源推荐
1. 教材回归:以课本例题和课后习题为蓝本,确保基础题满分。
2. 真题精练:近5年本地中考真题至少完成3遍,总结命题规律。
3. 专题资源:参考《九年级数学全年教案》《二次函数典型命题评析》等专项资料强化薄弱点。
附:核心公式速记
二次函数顶点式:( y = a(x-h)^2 + k )(顶点坐标((h,k)))。
弧长公式:( l = frac{npi r}{180} )(( n )为圆心角)。
方差公式:( s^2 = frac{1}{n}sum (x_i
bar{x})^2 ) 。
通过系统规划与针对性训练,学生可有效突破中考数学重难点,实现成绩稳步提升。


