基尔霍夫定律的验证:从理论到实践的科学探索
作为电路分析的核心基础,基尔霍夫定律自1845年提出以来,始终是理解复杂电路行为的金钥匙。定律的理论正确性必须通过严谨的实验验证才能确立其科学地位。本文通过实验设计、数据分析和误差溯源,系统阐述基尔霍夫电流定律(KCL)与电压定律(KVL)的验证过程,揭示其在现代电路研究中的深远意义。
一、理论基础与验证逻辑
基尔霍夫定律包含两个基本定理:节点电流守恒(ΣI=0)和回路电压平衡(ΣU=0)。其物理本质分别源于电荷守恒与能量守恒定律。实验验证的核心在于:
- 构建包含多支路、多节点的典型电路模型
- 通过精密仪器测量关键参数
- 对比理论计算与实测数据的吻合度
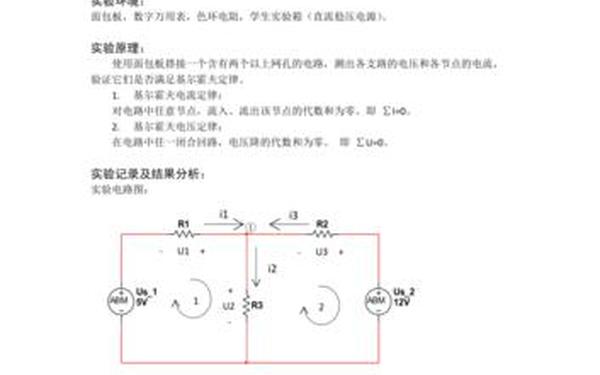
以图1所示经典三支路电路为例,理论计算需建立方程组:
I₁ + I₂ = I₃(KCL方程)
(510Ω+510Ω)I₁ +510ΩI₃=6V(KVL方程)

(1000Ω+330Ω)I₃=12V(KVL方程)
| 元件 | 参数 |
|---|---|
| 电源US1 | 6V DC |
| 电源US2 | 12V DC |
| 电阻R1-R3 | 510Ω, 1kΩ, 330Ω |
二、实验设计与操作规范
根据文献,标准实验流程包括:
- 仪器选型:选用0.5级精度的直流稳压电源、四位半数显万用表,确保测量误差≤±0.5%
- 电路搭建:
- 设定支路电流参考方向(如I₁流向节点A)
- 采用星型接线法减少接触电阻影响
- 数据采集:
- 电流表串联接入支路,注意红黑表笔极性匹配
- 电压表并联测量,遵循"红进黑出"原则
关键注意事项包括:电源输出需实测校准(理论值6V电源实测可能为5.98V),以及电阻元件的实际阻值测量(标称510Ω电阻实测常存在±5Ω偏差)。
三、数据验证与误差分析
某次典型实验数据如表2所示,节点A的KCL验证显示:
| 参数 | 理论值 | 实测值 |
|---|---|---|
| I₁ | 1.93mA | 2.08mA |
| I₂ | 5.99mA | 6.38mA |
| ΣI误差 | 0 | +0.54% |
误差主要来源于:
- 系统误差:仪表精度限制(如0.5级表±0.5%量程误差)
- 随机误差:接触电阻波动(约0.1-0.3Ω)导致电流分配变化
- 操作误差:参考方向误设引起的符号错误
四、仿真验证与实物对比
当实物实验受限于设备老化时(如某校实验室出现R₃支路测量失效),可采用Multisim进行数字仿真。对比研究发现:
| 验证方式 | KVL误差 | 优势 |
|---|---|---|
| 实物实验 | ≤7.77% | 真实物理现象观察 |
| 数字仿真 | ≤0.05% | 参数精确可控 |
但仿真无法完全替代实物操作,特别是接触电阻、温漂等非线性因素仍需实物验证。二者结合可形成完整的验证体系。
五、工程应用与未来方向
基尔霍夫定律在以下领域展现重要价值:
- 电力系统潮流计算(节点电压方程建立)
- 集成电路设计(寄生参数建模)
- 新能源并网控制(分布式电源协调)
未来研究方向包括:开发高精度原位测量技术(将误差控制在±0.1%内),以及拓展定律在纳米电路、量子器件等新兴领域的适用性边界研究。
通过系统化的实验验证,基尔霍夫定律的理论正确性得到充分证实。尽管存在测量误差等实践挑战,但其作为电路分析基石的学术地位不可动摇。建议教学实验中采用"实物操作+数字仿真"的双轨模式,并加强误差分析训练,以培养工程师的严谨科学思维。

