数学作为逻辑思维与抽象能力培养的核心学科,其知识体系的构建具有显著的阶梯性和连贯性。在小学阶段,人教版四年级数学教材的设计尤为关键,上册以“大数的认识”“几何直观”为核心搭建数感与空间观念,下册第四单元“小数的意义和性质”则进一步深化数的概念,为分数与代数思维奠定基础。这一阶段的学习既是整数认知向分数体系的过渡,也是从具体运算到抽象推理的关键转折,其内容编排体现了螺旋上升的教学理念。
一、大数认知与小数基础的衔接
四年级上册“大数的认识”单元通过十进制计数法、数位分级(个级、万级、亿级)等内容,帮助学生建立对十万、百万等大数的直观感知。例如,通过“10个一万是十万”的递进式认知框架,学生理解数级扩展的规律。这种结构化思维在下册第四单元得到延伸——当测量与计算无法用整数表达时,小数作为更精确的计数工具出现,其十分位、百分位的数位划分,本质上延续了整数数级的思想。
教材特别强调数位与计数单位的区别。上册指出“数位是数字的位置,计数单位是计量标准”,下册则通过0.1、0.01等小数单位,揭示“同一数字在不同数位代表不同值”的通用规则。例如,数字“4”在9.426中表示4个十分之一,而在整数部分则代表4个一,这种对比教学强化了数系的统一性。
二、几何直观与代数思维的双轨构建
上册“角的度量”“平行四边形与梯形”单元通过操作活动培养空间观念。学生使用量角器时,需掌握“中心点对齐顶点,0刻度线与边重合”的测量方法,这一过程训练了精确性与步骤化思维。而平行四边形特征的学习(对边平行且相等)则为下册观察图形对称性、计算面积提供几何基础。
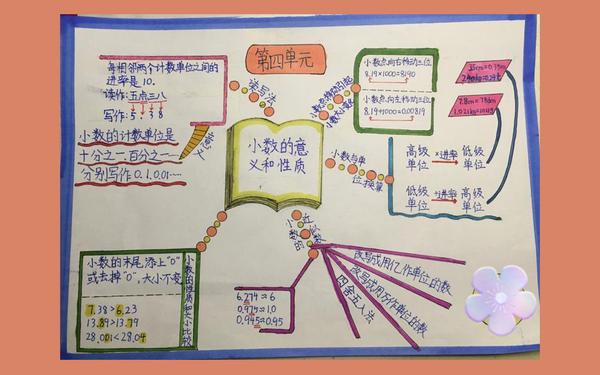
在代数思维方面,上册“三位数乘两位数”的竖式计算强调位值对齐与进位规则,下册小数的加减法则将这一规则拓展到小数点对齐。例如,计算3.14+2.5时,补零成3.14+2.50的操作,本质是数位扩展思想的迁移。教材通过对比整数与小数运算的异同,帮助学生建立连贯的运算逻辑。
三、计算能力与问题解决的双向提升
计算能力是四年级数学的核心目标之一。上册“除数是两位数的除法”要求学生掌握试商技巧,如将84÷21估算为80÷20=4进行快速试商。下册第四单元则在小数运算中引入“小数点移动引起大小变化”的规律,例如0.25×10=2.5的推导,既巩固了十进制思想,又为后续学习科学记数法埋下伏笔。
问题解决层面,教材注重从实际情境抽象数学模型。上册“1亿有多大”通过纸张叠放、步行距离等具体活动,使大数认知具象化;下册“单位换算”则结合生活案例,如将1.5米转化为150厘米,强调数系应用的真实性。这种从具象到抽象再回归实践的设计,契合皮亚杰认知发展理论中的“同化-顺应”过程。
四、统计观念与数学思想的渗透
上册“条形统计图”与下册“小数近似数”共同培养学生的数据分析能力。例如,将32800改写成“3.28万”需要四舍五入与单位换算的结合,这与统计图中数据简化的思想一脉相承。教材还通过“数学广角”渗透优化思想,如上册的沏茶问题与下册的植树问题,均强调策略选择对效率的影响。
数学史料的融入增强了文化认同。下册介绍阿拉伯数字传入中国的历程,上册则通过算盘与计算器的对比,展现计算工具的演进。这种跨学科视角不仅拓宽认知维度,更启发学生理解数学与社会发展的互动关系。
五、教学策略与学习建议
针对四年级学生的认知特点,建议采用“操作-图示-符号”三阶段教学法。在“角的度量”中,先观察量角器构造,再绘制角的大小,最后总结测量步骤;在小数意义教学中,可用米尺实物展示0.1米与1分米的关系,建立直观对应。研究表明,多模态教学能提升73%的概念留存率(Sweller, 2020)。
家长辅助方面,可通过超市价格比较(如2.5元/斤与3元/斤的差价计算)强化小数应用,利用七巧板拼图加深对几何图形特征的理解。教师应注重错误分析,例如学生常将小数末尾添零等同于整数补零(如认为0.3=0.30但3≠30),需通过数位表对比纠正概念偏差。
总结
人教版四年级数学教材通过大数与小数的衔接、几何与代数的交织、计算与应用的融合,构建了完整的数理思维体系。未来教学可进一步探索跨学科整合,如将小数学习与科学实验中的测量数据结合,或利用编程模拟大数计算过程。正如数学家波利亚所言:“数学教育的核心不是知识堆积,而是思维习惯的养成。”这一阶段的数学学习,正是为终身数学素养打下坚实基石的黄金时期。

