以下是八年级数学下册关于二次根式的概念及公式的教案设计,结合教材内容与教学目标,分模块进行阐述:
一、教学目标
1. 知识与技能
理解二次根式的定义,能判断一个式子是否为二次根式。
掌握二次根式有意义的条件,会求被开方数中字母的取值范围。
理解二次根式的双重非负性(被开方数非负,二次根式结果非负)。
掌握二次根式的性质及运算法则,能进行化简和简单运算。
2. 过程与方法
通过实际问题抽象出二次根式的概念,体会数学与生活的联系。
通过探究、讨论、练习,培养逻辑推理能力和运算能力。
3. 情感态度与价值观
激发对数学符号语言的学习兴趣,培养严谨的科学态度。
通过合作学习增强团队意识,感受数学的逻辑美与简洁美。
二、教学重点与难点
重点:二次根式的定义及有意义的条件;双重非负性;二次根式的化简。
难点:双重非负性的理解;分母有理化的运算技巧。
三、教学过程设计
1. 情境导入,引出概念
问题情境:
正方形面积为3,边长是多少?
自由落体时间公式 ( t = sqrt{frac{h}{5}} ),如何用含( h )的式子表示( t )?
面积为( S )的正方形边长为多少?
设计意图:通过实际问题引出形如( sqrt{a} )(( a geq 0 ))的式子,为定义二次根式做铺垫。
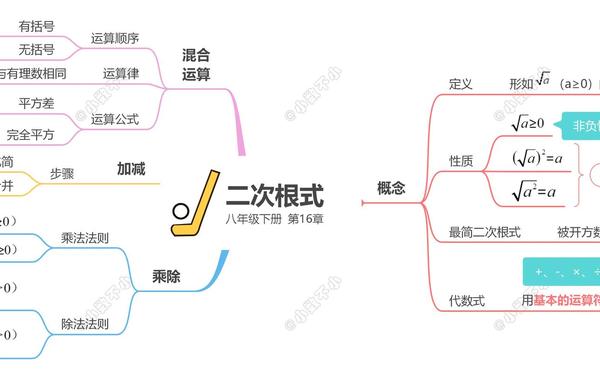
2. 抽象概括,形成概念
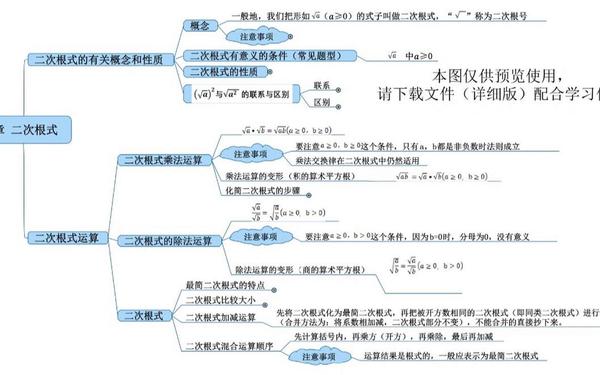
定义:形如( sqrt{a} )(( a geq 0 ))的式子称为二次根式,符号“√”称为二次根号,( a )为被开方数。
关键点:
被开方数必须是非负数(如( sqrt{2} )、( sqrt{x+1} ))。
双重非负性:( a geq 0 )且( sqrt{a} geq 0 )。
举例辨析:判断( sqrt{-3} )、( sqrt{x^2+1} )、( sqrt{frac{1}{2}} )是否为二次根式。
3. 探究性质,掌握公式
基本性质:
( (sqrt{a})^2 = a )(( a geq 0 ))。
( sqrt{a^2} = |a| )(结果为非负数)。
运算公式:
乘法:( sqrt{a} cdot sqrt{b} = sqrt{ab} )(( a geq 0, b geq 0 ))。
除法:( frac{sqrt{a}}{sqrt{b}} = sqrt{frac{a}{b}} )(( a geq 0, b > 0 ))。
加减法:需先化简为同类二次根式再合并(如( 2sqrt{3} + 3sqrt{3} = 5sqrt{3} ))。
4. 应用巩固,突破难点
例题1:求( x )的取值范围,使下列式子有意义:
( sqrt{x-2} )、( sqrt{frac{1}{x-5}} )、( sqrt{x^2+1} )。
解析:被开方数需非负,分母不为零。如( sqrt{frac{1}{x-5}} )要求( x > 5 )。
例题2:化简二次根式:
( sqrt{12} = 2sqrt{3} ),( sqrt{frac{18}{2}} = 3 )。
关键步骤:分解因数,提取完全平方数。
难点突破:分母有理化
例:( frac{1}{sqrt{2}} = frac{sqrt{2}}{2} ),通过分子分母同乘( sqrt{2} )消除分母中的根号。
5. 综合应用,提升能力
实际问题:
已知( x, y )满足( sqrt{x-2} + (y+3)^2 = 0 ),求( xy )的值。
等腰三角形两边长为( sqrt{8} )和( 3sqrt{2} ),求周长。
四、课堂小结与作业设计
小结:二次根式的定义、性质、运算及注意事项。
分层作业:
基础题:判断二次根式、求字母取值范围(如教材习题)。
提高题:化简复杂根式、分母有理化(如( sqrt{50} + sqrt{18} ))。
拓展题:结合勾股定理或几何图形设计应用题。
五、教学反思
通过实例抽象概念时,需关注学生是否理解“双重非负性”的逻辑关系。
在运算中,学生易混淆乘法分配律(如误认为( sqrt{a} + sqrt{b} = sqrt{a+b} )),需通过对比练习强化。
对于学困生,可设计更多具体数值的练习,逐步过渡到字母运算。
以上教案设计整合了多来源的教学策略,注重概念生成与运算能力的结合,可依据学生实际情况调整进度与难度。



