一、教学设计框架
1. 教学目标
知识与技能:理解有用功、额外功、总功的定义及关系;掌握机械效率的概念及计算公式;能结合具体机械(如滑轮组、斜面)分析效率影响因素。
过程与方法:通过实验探究(如斜面或滑轮组效率测量)设计实验方案,运用控制变量法分析数据,培养科学思维。
情感态度:认识机械效率的实际意义,如节能环保,激发创新改进机械的意识。
2. 教学重难点
重点:机械效率的定义与计算;实验探究影响效率的因素。
难点:区分有用功与额外功;理解机械效率永远小于1的原因。
3. 教学过程设计
导入:通过生活实例(如提水桶、用滑轮组运沙)创设情境,提问“使用机械是否省功”,引发认知冲突,引出效率概念。
概念生成:
分析实例(如滑轮组提升物体),明确有用功(提升物体)、额外功(克服摩擦、机械自重)、总功(动力做的功)。
公式推导:η=W有用/W总×100%,强调效率无单位且小于1。
实验探究:
滑轮组实验:测量不同物重、动滑轮重量下的η,分析效率变化规律。
斜面实验:改变斜面倾斜度或光滑度,观察η的变化,理解摩擦与倾角的影响。
巩固应用:
例题:计算滑轮组、斜面等场景的η,结合变形公式(如η=G物/(G物+G动))。
讨论:如何提高起重机、汽车引擎等机械的效率。
二、机械效率的5个核心公式及适用场景
1. 基础公式
[
eta = frac{W_{
ext{有用}}}{W_{
ext{总}}}
imes 100%
]
应用:所有机械通用,需明确区分有用功与总功。例如,提水时对水做的功为有用功,对桶做的功为额外功。
2. 滑轮组竖直提升物体
[
eta = frac{G_{
ext{物}}}{nF} quad
ext{或} quad eta = frac{G_{
ext{物}}}{G_{
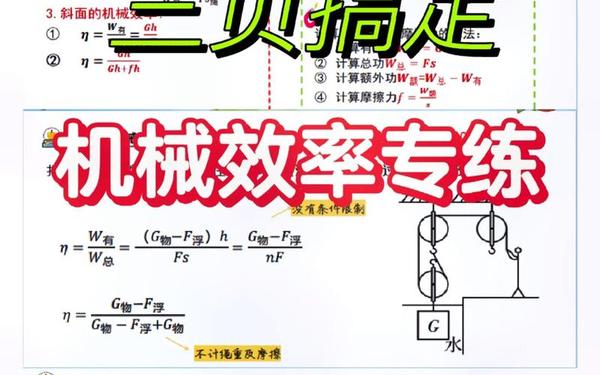
ext{物}} + G_{
ext{动}}}
]
说明:
( n )为滑轮组承担物重的绳子段数,( F )为拉力,( G_{
ext{动}} )为动滑轮重量。
公式变形体现物重与动滑轮重量对效率的影响,物重越大或动滑轮越轻,η越高。
3. 滑轮组水平拉动物体
[
eta = frac{f}{nF}
]
适用场景:水平匀速拉动物体时,有用功为克服摩擦力( f )做的功。
4. 斜面机械效率
[
eta = frac{Gh}{FL}
]
参数:( h )为斜面高度,( F )为拉力,( L )为斜面长度。斜面越光滑或倾角越大,η越高。
5. 杠杆机械效率
[
eta = frac{W_{
ext{有用}}}{W_{
ext{总}}} = frac{G cdot h_{
ext{物}}}{F cdot s_{
ext{动力}}}
]
说明:考虑杠杆自重时,额外功为克服杠杆重量所做的功。
三、教学策略与注意事项
实验设计:建议分组测量滑轮组效率,对比不同组的数据,讨论误差来源(如摩擦、测量精度)。
例题分析:
例1:用滑轮组提升80N物体,拉力为30N,机械效率为80%,求动滑轮重量。(答案:( G_{
ext{动}} = frac{G}{eta}
G = 20
ext{N} ))
例2:斜面长5m、高1m,用25N拉力拉动物体,机械效率60%,求物体重力。(答案:( G = eta cdot FL / h = 75
ext{N} ))
常见误区:
误认为省力机械效率高(实际省力可能增加额外功)。
混淆功率(做功快慢)与效率(能量利用率)。
四、引用来源与拓展
教学设计参考:
公式与实验:
应用案例:
通过以上设计,学生不仅能掌握公式计算,还能通过实验深化对机械能量转化的理解,培养解决实际工程问题的能力。


