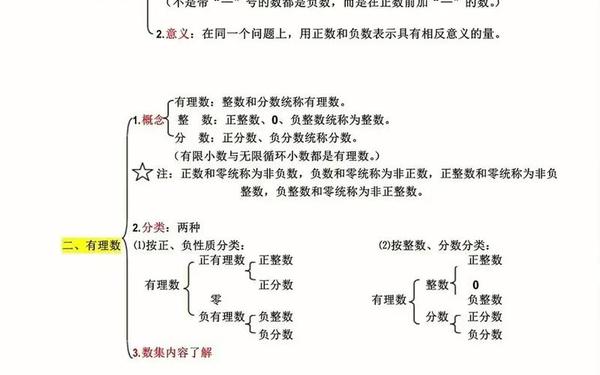
第一章 有理数
1. 正数与负数
正数:大于0的数;负数:小于0的数;0既不是正数也不是负数,是正负数的分界。
实际应用:表示相反意义的量(如温度、收支等)。
2. 数轴
三要素:原点、正方向、单位长度。数轴上的点与实数一一对应。
3. 相反数与绝对值
相反数:符号不同的两个数互为相反数(如5和-5),0的相反数是0。
绝对值:正数的绝对值是本身,负数的绝对值是其相反数,0的绝对值是0;几何意义是数轴上点到原点的距离。
4. 有理数的运算
加减法:同号相加取同号,异号相加取绝对值较大数的符号;减法转化为加法(加相反数)。
乘除法:同号得正,异号得负;除以一个数等于乘其倒数。
乘方:负数的奇次幂为负,偶次幂为正(如(-2)³=-8,(-2)²=4)。
5. 科学记数法
表示形式:( a
imes 10^n )(1≤|a|<10,n为整数),用于简化大数或小数的记录。
第二章 整式的加减
1. 单项式与多项式
单项式:仅含乘法运算的代数式(如( 3x^2 )),系数为数字因数,次数为字母指数和。
多项式:多个单项式的和,次数由最高次项决定(如( 2x^3 + x -1 )是三次多项式)。
2. 同类项与合并同类项
同类项:字母相同且指数相同的项(如( 3x^2 )与( -5x^2 ));合并时系数相加,字母部分不变。
3. 去括号法则
括号前是“+”号,括号内符号不变;括号前是“-”号,括号内符号全变(如( a-(b-c) = a-b+c ))。
第三章 一元一次方程
1. 方程基础
等式性质:等式两边加减/乘除同一数(非零),等式仍成立。
一元一次方程标准形式:( ax+b=0 )(a≠0)。
2. 解方程的步骤
去分母 → 去括号 → 移项 → 合并同类项 → 系数化为1。
3. 实际应用
常见题型:行程问题(路程=速度×时间)、工程问题(工作量=效率×时间)、利润问题(售价=定价×折扣)。
第四章 几何图形初步
1. 几何图形分类
立体图形(如长方体、圆柱)与平面图形(如线段、圆)。
展开图:某些立体图形可展开为平面图形(如正方体展开图)。
2. 点、线、面、体
点动成线,线动成面,面动成体;几何图形由点、线、面构成。
3. 直线与线段
公理:两点确定一条直线;两点之间线段最短。
线段中点:若点M是AB中点,则( AM = MB = frac{1}{2}AB )。
4. 角与角度计算
角的平分线:将角分为两个相等的角。
余角与补角:和为90°的角互余,和为180°的角互补。
易错点与学习方法
1. 绝对值与符号:处理负数运算时需注意符号变化,如( |-3|=3 ),( -(-5)=5 )。
2. 去括号时的符号:括号前有负号需改变括号内所有项的符号。
3. 方程检验:解方程后需代入原式验证解的合理性。
以上知识点可根据教材版本(人教版/北师大版)微调,但核心内容一致。建议结合习题强化运算与应用能力,并利用思维导图梳理章节联系。如需更详细例题或分章节练习,可参考文末来源。


