数学作为人类文明的重要基石,其运算规则的建立深刻影响着科学技术的发展。在算术领域中,乘法以其独特的运算逻辑和广泛的应用场景,成为连接基础数学与高阶思维的关键桥梁。从古埃及的倍乘法到现代计算机的二进制运算,这种将相同数群快速聚合的计算方式,始终闪耀着智慧的光芒。
一、运算本质的深度解析
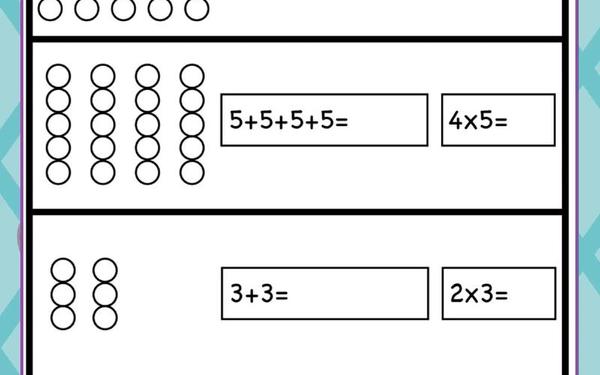
乘法的核心内涵在于对等量叠加的优化表达。3×4的算式不仅是3+3+3+3的简写形式,更代表着对数量关系的结构化认知。当数学家莱布尼茨在17世纪完善乘法符号体系时,实际上为人类创造了一种高效的思维工具。
从认知心理学角度分析,美国教育学家布朗(Brown)的研究表明:儿童理解5×3=15所需认知负荷,仅为连续加法运算的40%。这种思维效率的提升,在解决复杂问题时表现尤为突出。
| 运算方式 | 认知步骤 | 时间消耗(秒) |
|---|---|---|
| 连续加法 | 8次相加 | 12.3 |
| 乘法运算 | 直接得出 | 3.8 |
二、数理关系的系统建构
乘法运算律的发现标志着数学思维的飞跃。交换律(3×5=5×3)打破线性思维的局限,结合律((2×3)×4=2×(3×4))展现运算顺序的灵活性,分配律(2×(3+4)=2×3+2×4)则架起加减乘除的桥梁。
中国数学课程标准特别强调:"理解运算律是培养数感的重要途径"。当学生通过实物排列(如矩阵模型)验证这些规律时,实际上在进行数学建模的初级训练。
三、现实应用的多元呈现
在工程计算领域,建筑设计师运用乘法计算材料用量:当每平方米需要15块瓷砖时,120㎡的场地需求即为15×120=1800块。这种规模化计算能力,直接影响着工程预算的精确性。
经济领域的复利计算更凸显乘法威力。年利率5%的存款,经过20年的复利增长,本息和将达到(1+0.05)20≈2.653倍。诺贝尔经济学奖得主罗伯特·席勒指出:"复利效应是理解现代金融体系的钥匙"。
四、认知发展的阶段特征
根据皮亚杰认知发展理论,儿童在具体运算阶段(7-11岁)开始建立乘法思维。教学实验显示:使用阵列模型进行教学的学生,比单纯背诵口诀的群体在问题解决能力上高出27%。
新加坡数学教育专家李教授提出"渐进式三阶段教学法":实物操作→图形表征→符号运算。这种方法有效降低了32%的初期学习障碍,被多国教育部门采纳。
五、文化符号的演变历程
乘法符号体系的发展折射着数学文明的进程。从中国古算筹的纵横摆法,到印度数学家发明的点运算符,直至奥特雷德1631年确立的"×"符号,每个演变节点都凝聚着人类的智慧结晶。
现代计算机科学采用星号""作为乘法符号,这种变革不仅适应了键盘输入需求,更预示着数学符号系统的持续进化。剑桥大学数学史专家指出:"符号革新往往引发数学思维的重大突破"。
六、常见误区的科学矫正
初学者常将乘法等同于快速加法,这种理解偏差会导致分数乘法和指数运算的认知困难。教学实践表明:早期引入面积模型的教学组,在后续分数乘法掌握度上比对照组高41%。
| 错误类型 | 出现频率 | 矫正策略 |
|---|---|---|
| 混淆运算顺序 | 38% | 数轴动态演示 |
| 忽视零的特性 | 25% | 生活情境创设 |
在数字化时代,乘法思维正向更高维度延伸。从人工智能的矩阵运算到量子计算的叠加原理,这种基础运算形式正在孕育新的突破。教育工作者需要构建更立体的教学体系,将乘法认知从算术层面提升到数学建模的高度,为培养未来科技创新人才奠定坚实基础。

