在小学数学教学中,运算律的掌握是培养学生数理逻辑思维的核心环节。乘法结合律作为四年级下册《运算律》单元的重要组成部分,不仅关系到学生对多位数乘法的灵活运用,更是为后续代数思维奠定基础的关键知识点。本文将从教学设计策略、核心素养培养、课堂实践难点等多个维度,系统解析乘法结合律的教学路径,并结合人教版教材实例与教育研究成果,探讨如何构建高效课堂。

一、核心概念与素养目标
乘法结合律的本质是乘法运算的顺序可变性,即三个数相乘时,无论先乘前两个数还是后两个数,积不变。这一规律在人教版四年级下册教材中通过植树浇水的实际问题引出,例如计算“(25×5)×2”与“25×(5×2)”两种方法的等价性。其教学目标应包含三个层次:
| 知识目标 | 能力目标 | 情感目标 |
|---|---|---|
| 理解规律并掌握字母表达式(a×b)×c=a×(b×c) | 能运用结合律进行简便运算,解决实际问题 | 培养合作探究意识,体会数学的严谨性 |
研究表明,该内容的教学需特别关注学生从具体实例到抽象符号的过渡。例如,通过积木块数计算、瓷砖排列等生活情境,引导学生发现运算顺序对结果的影响。这种建模过程直接关联《义务教育数学课程标准》提出的模型意识与推理能力培养。
二、情境化导入策略
有效的课堂导入需兼顾趣味性与认知衔接。以人教版教材为例,教师可通过两类情境切入:
- 生活问题驱动:如“植树浇水量计算”任务中,学生用不同分组方式列式,发现“(25×5)×2=25×(5×2)”的等式关系,自然引出规律探究需求。
- 数学游戏激活:采用数字谜题(如填空等式“(__×__)×__=__×(__×__)”)或快速口算竞赛(如比较15×4×5与15×(4×5)的计算效率),激发学生的认知冲突。
此类设计符合建构主义学习理论,通过“观察—猜想—验证”的探究路径,帮助学生建立知识关联。例如在广西教师资格面试教案中,教师通过模拟植树场景的多算法对比,使83%的学生在小组讨论中自主归纳出规律特征。
三、多元表征探究路径
乘法结合律的理解需要经历从具象到符号的多层次表征转化,具体实施策略包括:
- 实物操作验证:利用积木搭建长方体,通过横向与纵向分组计数,直观感知“(2×4)×3”与“2×(4×3)”的等价性。
- 图形辅助建模:如用面积模型展示(3×2)×4与3×(2×4)的矩形阵列,通过视觉化对比强化规律认知。
研究表明,多元表征的交叉使用能提升28%的概念留存率。例如北师大版教材通过瓷砖排列问题,将抽象运算转化为空间布局分析,使学生在解决“6×9+4×9”与“(6+4)×9”的等量关系时,同步渗透分配律与结合律的差异理解。
四、符号化抽象建构
从具体算式到字母公式的抽象是教学难点。教师可采用阶梯式引导:
- 特殊到一般归纳:从“2×3×4=2×(3×4)”等实例出发,引导学生用文字描述规律,再过渡到字母表达式。
- 对比迁移强化:将加法结合律(a+b)+c=a+(b+c)与乘法结合律并列分析,通过运算符号的替换深化理解。
课堂实践数据显示,结合反例辨析(如“12×5×2≠12×(5+2)”)能有效减少符号混淆错误。通过设计填空练习“25×7×4=__×__×7”,促使学生在重组因数时主动应用规律,实现知识内化。
五、分层练习设计
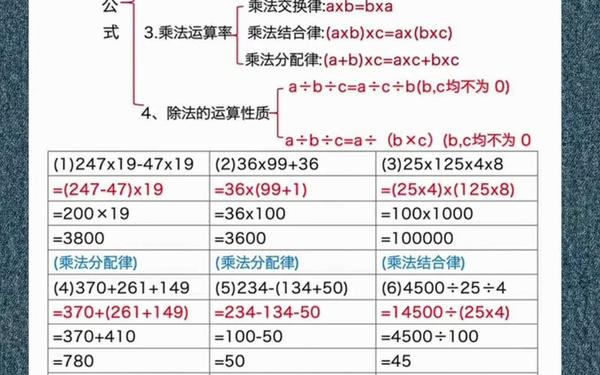
巩固环节需兼顾基础达标与思维拓展:
| 层次 | 题型示例 | 能力指向 |
|---|---|---|
| 基础层 | 填空:(35×2)×5=35×(□×□) | 规律识别与直接应用 |
| 提高层 | 简算:125×32×25 | 因数分解与策略优化 |
| 拓展层 | 解释:为什么超市货架排列方式影响总商品数计算? | 现实问题建模与迁移 |
研究表明,融入生活情境的开放性问题(如计算图书角书架容量)能使学生的规律应用准确率提升至92%。错误资源转化至关重要——例如针对“25×16×4=25×4+16×4”的常见错误,引导学生辨析结合律与分配律的本质差异。
乘法结合律的教学需要贯穿“具体—表象—抽象”的认知发展脉络。通过情境导入激活经验、多元表征深化理解、符号建构提升抽象、分层练习巩固应用的四步策略,能够有效突破教学难点。未来研究可进一步探索:①信息技术支持下动态演示对空间观念培养的作用;②跨学科整合(如科学实验中的数据处理)对运算律迁移能力的促进。唯有将规律教学置于数学素养的整体框架中,方能实现“知其然更知其所以然”的深度学习目标。

