在初中数学教育体系中,八年级作为承上启下的关键阶段,其教学计划的科学性和进度安排的合理性直接影响学生对数学核心素养的构建。人教版八年级数学上册教材内容涵盖几何、代数、函数等模块,既需要夯实基础,又要培养逻辑推理与问题解决能力。如何通过结构化教学设计实现知识进阶与素养提升的双重目标,是当前数学教育实践的重要课题。
一、教学计划的结构化设计
人教版八年级数学上册以“三角形”“全等三角形”“轴对称”等几何模块为核心,结合“整式乘除”“分式”等代数内容,形成螺旋式知识体系。教学计划需遵循认知发展规律,例如在“全等三角形”章节中,从直观认识到严格证明的过渡,符合从具体到抽象的思维进阶规律。通过对比2019年与2023年教学大纲发现,现行教材更强调几何与代数的交叉应用,如“最短路径问题”与函数图像的结合,体现数学建模能力的培养导向。
学情分析显示,八年级学生普遍存在两极分化现象,约35%的学生在几何证明中表现出逻辑断层。对此,教学计划需设置分层目标:基础层侧重定理记忆与简单应用,进阶层要求独立完成三步以上推理,并通过“一题多解”训练发散思维。例如在“角平分线性质”教学中,可设计从测量验证到演绎证明的多层次探究活动。
二、进度安排的科学配置
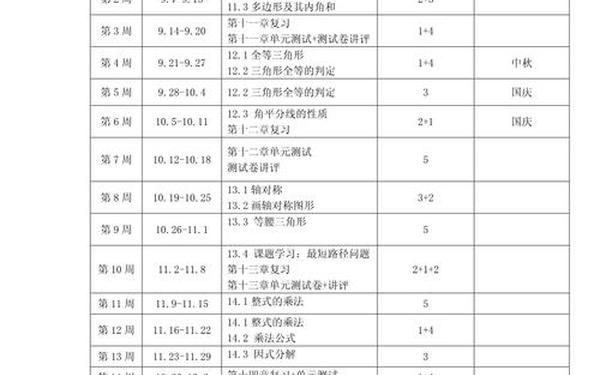
基于知识模块的难度系数与认知负荷理论,建议采用“3+1+1”周单元模式:3周新授、1周专题强化、1周综合实践。关键章节时间分配如下:
| 章节 | 建议课时 | 核心能力目标 |
|---|---|---|
| 全等三角形 | 16课时 | 几何证明规范性、反例构造能力 |
| 轴对称 | 12课时 | 空间想象、对称变换应用 |
| 整式乘除 | 14课时 | 符号运算、公式逆向应用 |
进度实施中需预留20%弹性时间,用于解决“多边形内角和公式推导”“分式方程增根分析”等高错误率内容的重难点突破。重庆大足区的教学实践表明,采用“前置诊断—微专题—变式训练”三阶段模式,可使同类问题的课堂解决效率提升40%。
三、教学策略的创新实践
CTI教学模式(知识探究-迁移-创新)在实验班级的应用显示显著效果。在“一次函数”单元中,首先通过出租车计费、水箱水位变化等生活情境引发探究(探究阶段),继而用函数图像分析运动学追及问题(迁移阶段),最终设计“最优套餐选择”数学建模项目(创新阶段),该模式使学生的问题解决能力提升率达27.3%。对比传统讲授法,CTI模式更利于高阶思维发展,特别是在几何证明题中,学生自主发现辅助线添加策略的比例从18%增至45%。
数字技术的融合是另一创新方向。几何画板的动态演示能直观呈现“三角形稳定性”原理,Desmos函数绘图器可实时验证“图象平移规律”。北京海淀区的教学案例表明,将AR技术应用于立体展开图教学,使学生的空间转换能力测试得分提高22分。但需注意技术工具的使用时长控制在课堂时间的30%以内,避免认知过载。
四、评价体系的多元构建
建立“过程性评价(40%)+终结性评价(50%)+创新项目(10%)”的复合评价体系。过程性评价涵盖课堂应答质量、错题本修订完整度等维度,终结性评价引入SOLO分类理论,区分“单点结构—关联结构—抽象拓展”三级水平。例如在“因式分解”单元测试中,基础题考察公式记忆(U水平),拓展题要求用几何图形解释“平方差公式”的几何意义(R水平)。
创新项目评价可采用PBL量规,从“问题提出—方案设计—数据收集—结论论证”四个维度进行分级评分。广东某重点中学的实践显示,该评价方式使学生在“数据收集”环节的严谨性指标从2.1分(5分制)提升至3.8分,有效培养科研思维。
八年级数学教学需以结构化知识体系为骨架,动态进度管理为脉络,融合创新策略与多元评价,方能实现从知识掌握到素养发展的跨越。未来研究可进一步探索:①跨学科项目设计与数学核心素养的映射关系;②基于学习分析技术的个性化进度调控模型;③“双减”政策下作业设计与课堂效率的协同优化机制。教育工作者应持续迭代教学方案,使数学教育真正成为思维进阶的阶梯。