登录
意见反馈
当前位置：首页 初中作文正文

动量定理教案;毕克定理两大公式

admin52025-03-19 09:34:21

1. 教学目标与核心素养

动量定理教案;毕克定理两大公式

  • 物理观念：理解动量定理的推导过程，掌握冲量概念，明确动量变化与合外力冲量的关系。
  • 科学思维：能用动量定理解释缓冲现象（如安全气囊、跳沙坑）及碰撞问题。
  • 科学探究：通过实验（如鸡蛋从不同高度掉落）观察动量变化与作用时间的关系，引导推导定理。
  • 科学态度：联系生活实例（如汽车刹车、高空跳海），培养物理与实际问题结合的意识。

    • 2. 教学重点与难点

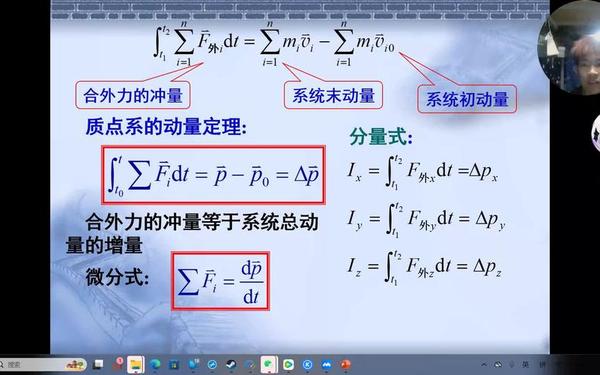
  • 重点：动量定理的推导（由牛顿第二定律 ( F = ma ) 结合匀变速公式得出 ( Ft = Delta p )）及矢量性理解。
  • 难点：变力冲量的计算（需用平均力或微元法）、动量定理方向一致性的理解。

    • 3. 教学过程设计

  • 导入实验：粉笔从高处落在水泥地与厚布上的对比实验，引发学生对作用时间与冲击力关系的思考。
  • 推导环节：
  • 从牛顿定律出发，结合匀变速公式 ( v = v_0 + at )，导出 ( F_{ ext{合}} t = Delta p ) 。
  • 通过 ( F-t ) 图像分析变力冲量的计算（面积法）。
  • 应用案例：
  • 缓冲原理：延长作用时间减小冲击力（如安全气囊、运动落地屈膝）。
  • 碰撞问题：解释短时作用力（如锤钉钉子）与动量变化的定量关系。
  • 练习设计：计算安全带平均冲击力（如质量60kg，缓冲时间1.2秒，( F_{ ext{avg}} = Delta p / t )）。

    • 二、毕克定理两大公式及应用

    毕克定理（又称皮克定理）用于计算格点多边形面积，分为以下两类网格：

    动量定理教案;毕克定理两大公式

    1. 正方形格点公式

  • 公式：( S = N + frac{L}{2}
  • 1 )
  • ( S )：多边形面积；
  • ( N )：内部格点数；
  • ( L )：边界格点数。
  • 示例：若多边形内部有8个格点，边界有20个格点，则面积 ( S = 8 + frac{20}{2}
  • 1 = 17 ) 。

    • 2. 三角形格点公式

  • 公式：( S = left( N + frac{L}{2}
  • 1 right) imes 2 )
  • 适用条件：网格由等边三角形构成，每个小三角形面积为1单位。
  • 示例：若内部有4个格点，边界有4个格点，则面积 ( S = left( 4 + frac{4}{2}
  • 1 right) imes 2 = 10 ) 。

    • 3. 应用场景

  • 快速计算不规则图形面积：如礼盒平面图、正六边形分割后的阴影面积计算。
  • 竞赛数学与编程题：常用于避免复杂几何运算，直接通过格点计数求解。

    • 参考资料

  • 动量定理教案设计参考：网页。

    • 毕克定理公式与应用案例：网页。

    文章下方广告位

    相关文章

    热门标签
    关注我们